Electronic beamforming uses a transducer array coupled with analog or digital signal processing circuitry to form beams. Sum and delay beamforming and narrowband phase-shift beamforming are two widely used algorithms implemented by the circuitry. The amount of signal processing circuitry and required power both increase with the number of transducers. This becomes a critical problem when large arrays are needed, especially for portable systems such as diver-held or autonomous underwater vehicle sonar systems.
Acoustic lenses implement beamforming with minimal associated circuitry. An acoustic lens focuses sound in much the same way that an optical lens focuses light. Snell's law describes the refraction of sound as it passes through an interface between two materials of differing sound speed. An acoustic lens provides the appropriate material thicknesses that focus a parallel wavefront of sound to a single focal point.
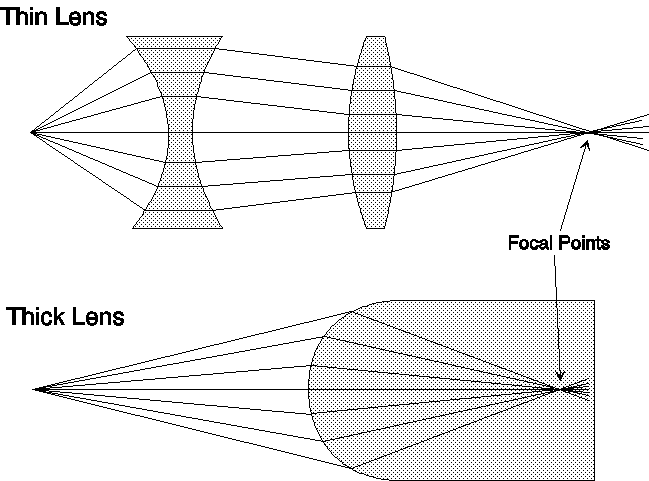
Acoustic lenses can be differentiated into two types: thick and thin. The focal point of a thick lens lies within the lens material, whereas the focal point of a thin lens is outside of the lens material (Figure 1). Either type may be a compound lens, with multiple layers of materials of differing refractive indices. Compound lens systems can be designed to optimally focus sound from several source directions or to reduce the sensitivity of the system to varying ambient temperatures.
Two methods of implementing wave acoustics have been proposed. The first is to numerically integrate the Kirchhoff integral, thereby approximating the solution. The second method is to use the underlying principle behind the Kirchhoff integral, the Huygens-Fresnel theory. The resulting implementation involves summing the contributions of virtual point sources to find the solution at a specific point in space.
Cornelius & Williams examined the pressure field formed behind a hemispherical thick acoustic lens. 11 Their method incorporates concepts from both geometrical and wave acoustics to calculate the pressure field behind the lens. In order to calculate the complex pressure field, the Kirchhoff integral is numerically integrated using pressures generated by ray tracing for boundary values.
Mr. Donald Folds of ARINC Corporation also developed a software simulator for acoustic lenses. 12 It uses a similar hybrid geometric/wave approach, but employs a different method to calculate the pressure field. Rather than integrating the Kirchhoff integral, it directly calculates the pressure field by summing the contributions of virtual point sources on the final lens surface. Direct summation replaces numerical integration and the complex pressures on the final lens surface act as boundary values. The magnitude and phase of the virtual point sources are generated by ray tracing, as in the integration scheme.
Other efforts have been made to simulate the beam patterns of specific acoustic lenses using similar methods. Folds simulated a variety of lens systems, including a cylindrical liquid-filled (thick) lens 15, 16 , a four-element thin lens 13 , and a variety of cylindrical single and multi-element thin lenses 14. Beaver, Dameron, and Macovski simulated a single-element thin acoustic lens operating at 2.25 MHz. 3 Oh and Park simulated the beam pattern of a lens system that included both a thin lens mounted on the transducer element and a reflector 19, 20.
Other methods have also been used to find sound pressure levels near a lens. Makarchenko, Rozhin, and Tonakanov investigated a liquid spherical lens using the exact solution of the Kirchhoff integral 18. Penttinen and Luukkala transformed a single-surface lens into a curved transducer having the same focusing properties as the lens. They then used the rapid impulse method to compute the pressure distribution 21.
ALSSP includes both the numerical integration method used by Cornelius and Williams and the summation method used by Folds and others. The integration method assumes that the lens system is radially symmetric and exploits that symmetry in order to provide increased execution speeds. However, this restricts its applications to radially symmetric lens systems with on-axis sources. The summation method does not make any assumptions about the lens system or source location, so is more universally applicable. The ray tracing can be confined to two dimensions when desired in order to speed analysis, but is performed in three dimensions by default. Due to the decreased number of intermediary steps required, the summation method is also much quicker than the numerical integration method.
The primary contribution of this software set is its generality. It can analyze any of the lens systems discussed above (with the exception of the reflector system analyzed by Oh and Park) and can also show the effects of varying system environment parameters such as water temperature, salinity, and frequency of operation.
Acoustic lens design uses the same methods as optical lens design. These methods rely on ray tracing, which is a geometrical concept providing an approximation to the true behavior of the lens. The accuracy of the approximation depends on the size of the lens system with respect to the wavelength of light or sound passing through it. For most optical systems, this ratio is very large, providing a good approximation. However, the wavelength of sound in most acoustic applications is significant with respect to realistic lens sizes, and thus the geometrical approximations do not work as well.
Wave acoustics theory provides a more accurate description of the behavior of sound, but is more complicated. The integral equations that describe sound propagation across interfaces in wave acoustics are often difficult or impossible to solve in closed form, and require substantial processing time to solve numerically.
The simulation implemented in ALSSP uses geometrical acoustics within the lens system and wave acoustics in the focal region. The transformation from geometrical to wave acoustics occurs at a point where both are feasible and accurate; the final lens interface. Geometrical acoustics, realized by ray-tracing, calculates the complex pressures on the final lens interface. Wave acoustics uses those pressures as boundary values in order to solve the Kirchhoff integral, which gives the pressure at points in the focal region.
The ray-tracing code included in ALSSP neglects the reflected component of rays. It has been experimentally determined that shell thicknesses of odd quarter wavelengths attenuate the sound pressure more than shell thicknesses of even quarter wavelengths 9. This is probably an effect of interference due to reflection within the shell, and thus is not modelled by this simulation.
Return to Title Page and Table of Contents
kevin@fink.com