Lens systems may have any number of components placed arbitrarily in three dimensional space. The lens interfaces are planar, spherical, or aspherical, which includes hyperboloids, paraboloids, and ellipsoids. The density, sound attenuation rate, and sound speed of each lens material are also specified. Sound sources available are point sources, planar sources, and curved linear sources, while receive element types are point, rectangular, curved rectangular, and circular. The ray-tracing algorithms accommodate any number of rays, in either two or three dimensions. Plots of lens systems, with or without traced rays, may be viewed on the screen and/or printed.
ALSSP has the capability to calculate pressure fields, find focal points, and generate beam patterns. Pressure fields may be generated in several types of regions, including planar circles and rectangles, curved rectangles (i.e. cylinder sections), and rectangular volumes. Focal points may be found along lines or in rectangular regions of space. Beam patterns may be generated along lines, arcs, or piecewise-circular trajectories and include the effects of the receive element.
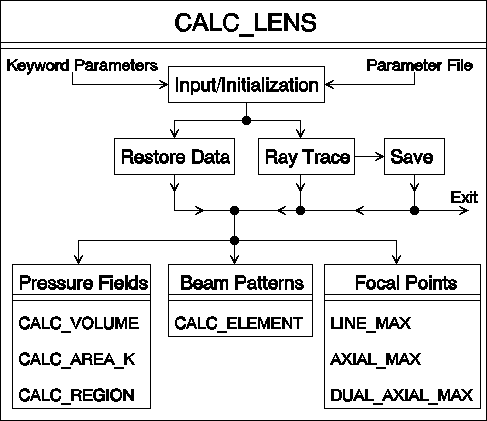
The main program module of ALSSP is CALC_LENS. A block diagram is shown in Figure 9. Keyword parameters and a parameter file contain information on the lens system and type of calculation desired. The ray trace data is restored if previously saved, otherwise the ray trace is performed. The data can be saved at that point for later use. CALC_LENS then calls the appropriate module for the type of calculation desired.
The lens system operates underwater. The system depth, water salinity, attenuation rate of sound in the water, density of the water, ambient water temperature, and system frequency must be specified. The speed of sound in the surrounding water can be specified in meters/second or the program will calculate it using the water depth, salinity, and temperature, using the formula 10
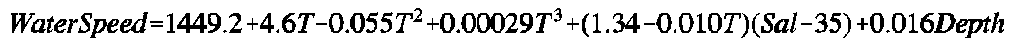
where
The main program, CALC_LENS, takes a number of control parameters that specify how the results will be computed and stored, and how errors and other information will be logged. The program uses the summation method of calculating the pressure by default, but can also use the numerical integration method. The number of rays to trace must be specified. Ray tracing is done in three dimensions by default, but can be constrained to a plane if desired.
If the ray trace is to be displayed, the title, x and y ranges, axis titles, tick sizes, and plot color can be specified. The y-range can also be automatically set from the x-range to preserve a square aspect ratio (so that circles look like circles instead of ellipses). ALSSP can also display only a fraction of the rays that are actually traced in order to produce a less cluttered plot while preserving the accuracy of the calculations. Similarly, the ray plot can be restricted to the z=0 plane instead of projecting all rays into that plane.
A number of files may be specified in order to control how CALC_LENS computes and stores its results. The ray trace results can be saved independently of any other results and then restored later, so that calculations do not need to redo previously computed ray traces. In conjunction with this, the program can be told to compute ray trace results and save them but not to perform any additional calculations. The logging information that is normally displayed on the screen can be sent to a log file for later reference. The verbosity of the logging information can also be controlled. The file name that holds the calculated pressure field or beam pattern can be specified, although it defaults to the name of the input parameter file with '.out' appended to the end. In addition, CALC_LENS can be commanded to enter view mode, in which the ray trace is displayed with 21x21 rays (or 21 rays for a 2D trace) and no results at all are saved or logged.
The traced rays originate at a source, which can be a point, plane, or a curved or straight line. The usual type is a point source, in which all the rays emanate from a single point in space. In a planar source all incoming rays are parallel, which is equivalent to a point source at an infinite distance. The final type of source is a curved, linear source, defined by a set of equally spaced point sources arrayed along a curved line. The curvature of the line is set to 0 for a linear source.
The lens system consists of any number of lenses, each specified by its interfaces. Interface types are planar, spherical, ellipsoidal, and aspherical. The aperture of each interface specifies the region through that rays may pass. Rays outside of the interface's aperture will be discarded. The material after each interface is specified by its sound speed, density, and sound attenuation rate.
A planar interface is specified only by its origin and aperture size, and thus is actually a circle in the yz-plane. Spherical and ellipsoidal interfaces are special cases of aspherical interfaces. Aspherical lens surfaces are spherical with an added shape factor that allows different conic classes 1.
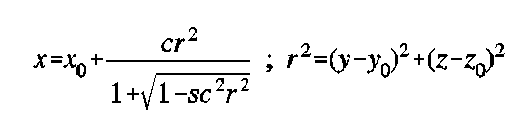
The curvature c is specified by 1/(radius of curvature at the center). The shape factor s can be:
ALSSP calculates complex pressure fields along a line, an arc, a calculated trajectory, or in a region of space. It also finds the focal point of a lens system along a line or in a plane. In addition, an element can be placed in the pressure field in all of the above calculations.
A beam pattern is a plot of magnitude vs. source angle: a plot of the response of a fixed transducer element to a moving point source. Calculating a beam pattern requires doing a separate ray trace and complex summation or integration for each source angle, which is computationally expensive. However, the beam pattern can be approximated by fixing the source and moving the element instead.
This approximation is very good in some cases, but falls short in others. The accuracy depends on the shape of the trajectory of focal points generated by moving the source. If the element is moved along this trajectory, the approximation will be very good. However, if the element is moved along a different trajectory, or the position along the trajectory is not correctly matched to the angles that generated it, the beam pattern will be inaccurate.
If the focal trajectory has only a small amount of curvature relative to the width of the desired beam pattern, a line cut through the pressure field may provide a good approximation to the true focal trajectory. The approximation can be improved by finding an arc that follows the focal trajectory.
One method is to find the center of curvature and radius of an arc by finding
the focal points due to two point sources, one on-axis and the other off-axis, and
assuming that the center of curvature is on the principle axis of the lens system
(Figure 10). The position of the center of curvature H" is called the secondary
principal point. It is defined as the point that generates an arc radius forcing the arc
angle to be equal to the source angle. With H" set, moving the
transducer element
 degrees is the same as moving the source
degrees is the same as moving the source
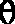 degrees. The radius of the arc is then set
so the arc includes the focal point that generated it, which is assumed to be the center
of the desired beam pattern.
degrees. The radius of the arc is then set
so the arc includes the focal point that generated it, which is assumed to be the center
of the desired beam pattern.
When the lens system has a focal trajectory with a more complicated curvature, moving the element along the focal trajectory will generate a better approximation of the beam pattern. In order to do this, the trajectory must be calculated by finding the focal points due to a number of source angles. Then the trajectory is approximated by a piecewise-circular function. (See the ALSSP User's Guide for more information.)
ALSSP will calculate pressures in a region of space. The region can be a rectangular volume, a planar rectangle or circle, or a curved rectangle (a section of a cylinder.)
A volume of space is specified by its origin (center), its size in three dimensions, and its sampling density in each dimension. Setting the size in one or more dimensions equal to zero selects a rectangular or linear region of space.
Each of the other three regions are planar (or planar with a curve), and are specified by their origin, size, sampling density, and orientation. There are two ways to define a region's orientation in space. The simplest is by specifying the plane in which it lies: xy, xz, or yz. In these cases the sizes are specified directly in terms of the plane in which the region lies. If the xy plane is specified, then the first size refers to the x-direction and the second to the y-direction. Similarly, if the yz plane is specified, then the first refers to the y and the second to the z.
For more general orientations, the region's normal can be specified to define the direction in which the region faces. A normal of [0,-1,0] (parallel to the y-axis) would put the region in the x-z plane, and a normal of [-1,-1,0] would put the region parallel to the z-axis with its projection into the x-y plane a line with 45 degree angle (Figure 11).
Since the region is assumed to start in the y-z plane, care must be taken to specify the size correctly if another plane is desired. For example, for a rectangular region in the x-y plane with size in the x-direction of 10 cm and size in the y-direction of 5 cm, the orientation vector will be [0,0,1], but the size should be specified as 5,10 rather than 10,5, since the region will rotate around the y-axis, moving the second dimension from z to x but leaving the first as y.
A rectangle is specified by its origin (center), its size in two dimensions, the sampling density on its surface (in each dimension), and its orientation in space. A curved rectangle is a section of a cylinder wall, i.e. a rectangle that is curved in one dimension. A planar circle is specified identically to a rectangle, with the substitution of its radius for the rectangle's dimensions.
3.7.3 Focal Point Determination
The focal point of a lens system is defined as the point of maximum absolute pressure. The focal point can be found along a line or in a plane. The algorithm to find the focal point along a line is much faster than that for a plane, so should be used whenever possible.
In either case, a coarse search is done first over the search range in order to find a point near the global maximum, thus avoiding local maxima. Then the maximum is refined using a binary search until the accuracy condition is met. The accuracy is the distance between the maximum and the nearest two search points.
The planar algorithm finds the maximum parallel to the first axis at a fixed distance from the second axis (given by the initial guess.) Then it uses that point as the fixed distance from the first axis, and searches parallel to the second axis. This is repeated until the given accuracy is achieved. The algorithm is very slow to converge when searching along a ridge that lies at an angle to both axes, so when the maximum is known to lie along a certain line, it is much faster to search along that line. For example, in a single-element lens, the focal point will lie on the line extending from the source through the center of the lens.
Four element types are available. The first, a point element, represents the actual pressure level at a point in space. The other three (rectangular, curved rectangular, and circular) represent the effect of placing a receive element of a certain size and shape at a point in the pressure field. Each element is specified by its center, with the additions of size in each dimension for the rectangular elements and the radius of the circular element. The radius of curvature in each dimension must also be specified for the curved rectangular element, which is simply a smaller version of a curved rectangular region, described in section 3.7.2.
3.9 Element Orientation and Sampling Density
For any element except a point element, the element's orientation and sampling density must also be specified. The element can be oriented in one of two ways: so that it is always facing a specified direction, or so that it always faces a specific point, regardless of the element's position. In the first case, the orientation direction is specified identically to that of a rectangular pressure field (see section 3.7.2 and Figure 11).
Elements are approximated by summing the complex pressure field over the element's face, so the number of samples taken on the element's face must also be indicated. The accuracy of the approximation will increase with the number of samples, but the speed will decrease proportionately. Large elements require more samples than small elements. No general rule has been determined for choosing the number of samples on an element, but in practice it is easy to run trials with several sampling densities to determine when the response stops changing.
Return to Title Page and Table of Contents
kevin@fink.com